Эллипс. Фокусы. Уравнение эллипса. Фокусное расстояние.

Большая и малая оси эллипса. Эксцентриситет. Уравнение

касательной к эллипсу. Условие касания прямой и эллипса.

 

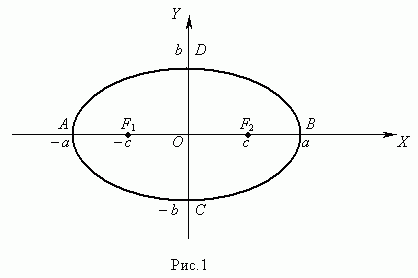
Эллипсом ( рис.1 ) называется геометрическое место точек, сумма расстояний от которых до двух заданных точек  F₁ и  F₂ , называемых  фокусами эллипса, есть величина постоянная.

Уравнение эллипса ( рис.1 ) :

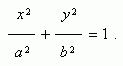
Здесь начало координат является центром симметрии эллипса, а оси координат – его осями симметрии. При  a > b фокусы эллипса лежат на оси ОХ  ( рис.1 ) , при  a < b  фокусы эллипса лежат на оси ОY , а при  a = b  эллипс становится окружностью ( фокусы эллипса в этом случае совпадают с центром окружности ). Таким образом,  окружность есть частный случай эллипса.

Отрезок  F₁F₂ = 2 с ,  где , называется фокусным расстоянием. Отрезок  AB = 2 a называется большой осью эллипса, а отрезок  CD = 2 b – малой осью эллипса. Число  e = c / a ,  e < 1 называетсяэксцентриситетом эллипса.

 

Пусть  Р ( х₁ ,  у ₁ ) – точка эллипса, тогда  уравнение касательной к эллипсу в данной точке имеет вид:

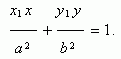
Условие касания прямой  y = m x + k  и эллипса  х ² / a ²  +  у  ² / b ²  = 1 :

 

 

k ²  = m ² a ² + b ² .