Треугольник. Остроугольный, тупоугольный и прямоугольный треугольник.
Катеты и гипотенуза. Равнобедренный и равносторонний треугольник.
Основные свойства треугольников. Сумма углов треугольника.
Внешний угол треугольника. Признаки равенства треугольников.
Признаки равенства прямоугольных треугольников.
Замечательные линии и точки в треугольнике: высоты, медианы,
биссектрисы, срединныe перпендикуляры, ортоцентр,
центр тяжести, центр описанного круга, центр вписанного круга.
Теорема Пифагора. Соотношение сторон в произвольном треугольнике.
Треугольник – это многоугольник с тремя сторонами (или тремя углами). Стороны треугольника обозначаются часто малыми буквами, которые соответствуют заглавным буквам, обозначающим противоположные вершины.
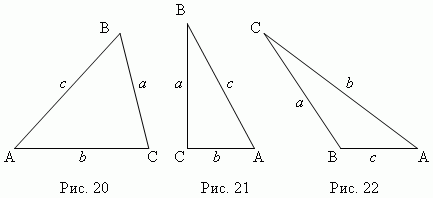
Если все три угла острые ( рис.20 ), то это остроугольный треугольник. Если один из углов прямой ( 
C, рис.21 ), то это прямоугольный треугольник; стороны a, b, образующие прямой угол, называются катетами; сторона c, противоположная прямому углу, называется гипотенузой. Если один из углов тупой ( B, рис.22 ), то это тупоугольный треугольник.
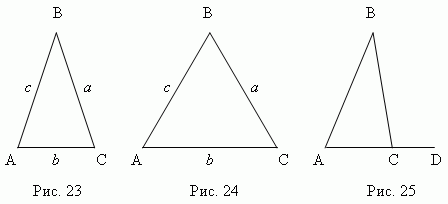
Треугольник ABC ( рис.23 ) - равнобедренный, если две его стороны равны ( a = c ); эти равные стороны называются боковыми, третья сторона называется основанием треугольника. Треугольник ABC ( рис.24 ) – равносторонний,если все его стороны равны ( a = b = c ). В общем случае ( a ≠ b ≠ c ) имеем неравносторонний треугольник.
Основные свойства треугольников. В любом треугольнике:
1. Против большей стороны лежит больший угол, и наоборот.
2. Против равных сторон лежат равные углы, и наоборот.
В частности, все углы в равностороннем треугольнике равны.
3. Сумма углов треугольника равна 180 º .
Из двух последних свойств следует, что каждый угол в равностороннем
треугольнике равен 60 º.
4. Продолжая одну из сторон треугольника (AC, рис.25), получаем внешний
угол BCD. Внешний угол треугольника равен сумме внутренних углов,
не смежных с ним: BCD = A + B.
5. Любая сторона треугольника меньше суммы двух других сторон и больше
их разности ( a < b + c, a > b – c; b < a + c, b > a – c; c < a + b, c > a – b ).
Признаки равенства треугольников.
Треугольники равны, если у них соответственно равны:
a) две стороны и угол между ними;
b) два угла и прилегающая к ним сторона;
c) три стороны.
Признаки равенства прямоугольных треугольников.
Два прямоугольных треугольника равны, если выполняется одно из следующих условий:
1) равны их катеты;
2) катет и гипотенуза одного треугольника равны катету и гипотенузе другого;
3) гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого;
4) катет и прилежащий острый угол одного треугольника равны катету и прилежащему острому углу другого;
5) катет и противолежащий острый угол одного треугольника равны катету и противолежащему острому углу другого.
Замечательные линии и точки в треугольнике.
Высота треугольника - это перпендикуляр, опущенный из любой вершины на противоположную сторону ( или её продолжение ). Эта сторона называется основанием треугольника. Три высоты треугольника всегда пересекаютсяв одной точке, называемой ортоцентром треугольника. Ортоцентр остроугольного треугольника ( точка O, рис.26 ) расположен внутри треугольника, а ортоцентр тупоугольного треугольника ( точка O, рис.27 ) – снаружи; ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла.
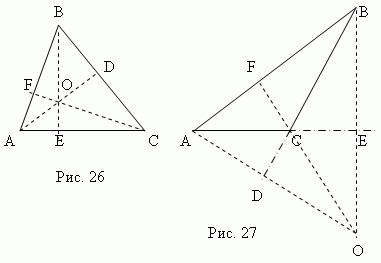
Медиана – это отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Три медианы треугольника ( AD, BE, CF, рис.28 ) пересекаются в одной точке O, всегда лежащей внутри треугольника и являющейся его центром тяжести. Эта точка делит каждую медиану в отношении 2:1, считая от вершины.
Биссектриса – это отрезок биссектрисы угла от вершины до точки пересечения с противоположной стороной. Три биссектрисы треугольника ( AD, BE, CF, рис.29 ) пересекаются в одной точке О, всегда лежащей внутри треугольника и являющейся центром вписанного круга (см. раздел «Вписанные и описанные многоугольники»).
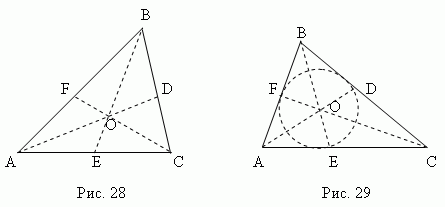
Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам; например, на рис.29 AE : CE = AB : BC .
Срединный перпендикуляр – это перпендикуляр, проведенный из средней точки отрезка (стороны). Три срединных перпендикуляра треугольника АВС ( KO, MO, NO, рис.30 ) пересекаются в одной точке О, являющейся центромописанного круга ( точки K, M, N – середины сторон треугольника ABC ).
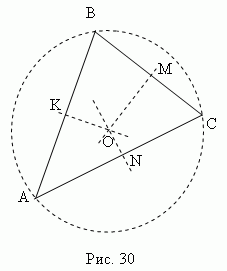
В остроугольном треугольнике эта точка лежит внутри треугольника; в тупоугольном – снаружи; в прямоугольном - в середине гипотенузы. Ортоцентр, центр тяжести, центр описанного и центр вписанного круга совпадают только в равностороннем треугольнике.
Теорема Пифагора. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Доказательство теоремы Пифагора с очевидностью следует из рис.31. Рассмотрим прямоугольный треугольник ABC с катетами a, b и гипотенузой c.
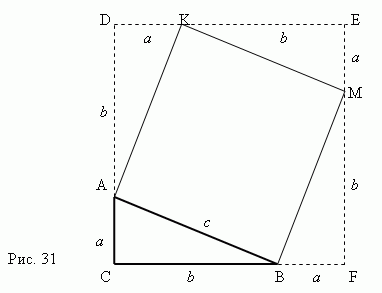
Построим квадрат AKMB, используя гипотенузу AB как сторону. Затем продолжим стороны прямоугольного треугольника ABC так, чтобы получить квадрат CDEF, сторона которого равна a + b . Теперь ясно, что площадь квадрата CDEF равна ( a + b ) 2. С другой стороны, эта площадь равна сумме площадей четырёх прямоугольных треугольников и квадрата AKMB, то есть
c 2 + 4 ( ab / 2 ) = c 2 + 2 ab ,
отсюда,
c 2 + 2 ab = ( a + b ) 2 ,
и окончательно имеем:
c 2 = a 2 + b 2 .
Соотношение сторон в произвольном треугольнике.
В общем случае ( для произвольного треугольника ) имеем:
c 2 = a 2 + b 2 – 2ab · cos C,
где C – угол между сторонами a и b .