Интегрирование по частям.

  Интегрирование подстановкой ( замена переменной ).

Интегрирование по частям. Если функции  u ( x )  и  v ( x ) имеют непрерывные первые производные и существует интеграл  v ( x ) du ( x ), то существует и интеграл  u ( x ) dv ( x ) и имеет место равенство:
 

 u ( x ) dv ( x ) = u ( x ) • v ( x ) –  v ( x ) du ( x )

или в более короткой форме:

 u dv = u v –  v du .

Обратите внимание, что интегрирование по частям и дифференциал произведения являются взаимно обратными операциями (проверьте!).

П р и м е р .	Найти интеграл:  ln x dx .
Р е ш е н и е.	Предположим u = ln x и dv = dx, тогда du = dx/x и v = x. Используя формулу интегрирования по частям, получим:

Интегрирование подстановкой (замена переменной). Если функция  f ( z ) определена и имеет первообразную при  z  Z ,  а  функция  z = g ( x ) имеет непрерывную производную при  x  X  и её область значений  g ( X )  Z , то функция  F ( x ) =  f  [ g ( x )] × g' ( x ) имеет первообразную на  Х  и

 F ( x ) dx =  f [ g ( x )] • g' ( x ) dx =  f ( z ) dz .

П р и м е р .	Найти интеграл: .
Р е ш е н и е.	Чтобы избавиться от квадратного корня, положим 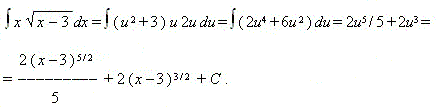 ,  тогда  x = u2 + 3  и, следовательно,  dx = 2u du. Делая подстановку, имеем: