Если функция  f ( x ) имеет первообразную на промежутке  X, и  k – число, то

Короче: постоянную можно выносить за знак интеграла.

Если функции  f ( x )  и  g ( x ) имеют первообразные на промежутке  X , то

Короче: интеграл суммы равен сумме интегралов.

Если функция  f ( x ) имеет первообразную на промежутке X , то для внутренних точек этого промежутка:

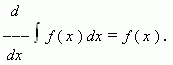
Короче: производная от интеграла равна подынтегральной функции.

Если  функция  f ( x )  непрерывна на промежутке  X  и дифференцируема во внутренних точках этого промежутка, то:

Короче: интеграл от дифференциала функции равен этой функции плюс постоянная интегрирования.