Вписанный в круг многоугольник.

Описанный около круга многоугольник.

Описанный около многоугольника круг.

Вписанный в многоугольник круг.

Радиус вписанного в треугольник круга.

Радиус описанного около треугольника круга. 
Правильный многоугольник.

Центр и апофема правильного многоугольника.
Соотношения сторон и радиусов правильных многоугольников.

 

 

Вписанным в круг называется многоугольник, вершины которого расположены на окружности ( рис.54 ). Описанным около круга называется многоугольник, стороны которого являются касательными к окружности

( рис.55 ).

 

 

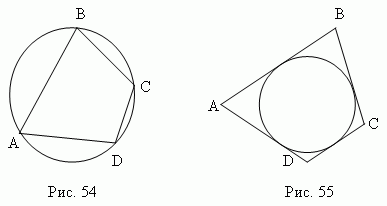
Соответственно, окружность, проходящая через вершины многоугольника ( рис.54 ), называется описанной около многоугольника; окружность, для которой стороны многоугольника являются касательными ( рис.55 ), называется вписанной в многоугольник. Для произвольного многоугольника невозможно вписать в него и описать около него окружность. Для треугольника это всегда возможно.

Радиус r  вписанного круга выражается через стороны  a, b, c  треугольника:

 

 

Радиус R описанного круга выражается формулой:

 

 

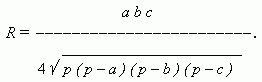
В четырёхугольник можно вписать окружность, если суммы его противоположных сторон равны. Для параллелограммов это возможно только для ромба ( квадрата ). Центр вписанного круга расположен в точке пересечения диагоналей. Около четырёхугольника можно описать круг, если сумма его противоположных углов равна 180º. Для параллелограммов это возможно только для прямоугольника ( квадрата ). Центр описанного круга лежит в точке пересечения диагоналей. Вокруг трапеции можно описать круг, если только она равнобочная.

 

Правильный многоугольник – это многоугольник с равными сторонами и углами.

 

 

 

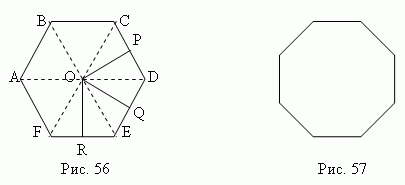
На рис.56 показан правильный шестиугольник, а на рис.57 – правильный восьмиугольник. Правильный четырёхугольник – это квадрат; правильный треугольник – равносторонний треугольник. Каждый угол правильного многоугольника равен 180º ( n – 2 ) / n , где n – число его углов. Внутри правильного многоугольника существует точка O ( рис. 56 ), равноудалённая от всех его вершин ( OA = OB = OC = … = OF ), которая называется центром  правильного многоугольника. Центр правильного многоугольника также равноудалён от всех его сторон  ( OP = OQ = OR = … ). Отрезки OP, OQ, OR, … называются апофемами; отрезки OA, OB, OC, …– радиусы правильного многоугольника. В правильный многоугольник можно вписать окружность и около него можно описать окружность. Центры вписанной и описанной окружностей совпадают с центром правильного многоугольника. Радиусописанного круга - это радиус правильного многоугольника, a радиус вписанного круга - его апофема. Соотношения сторон и радиусов правильных многоугольников:

 

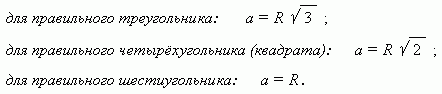
Для большинства правильных многоугольников невозможно выразить посредством алгебраической формулы соотношение между их сторонами и радиусами.

 

П р и м е р .   Можно ли вырезать квадрат со стороной 30 см из круга

                       диаметром 40 см?

 

Р е ш е н и е .  Наибольший квадрат, заключённый в круг, есть вписанный

                         квадрат. В соответствии с вышеприведенной формулой его

                         сторона равна:

 

                        

                         Следовательно, квадрат со стороной 30 см невозможно вырезать

                         из круга диаметром 40 см.