Приближённое решение неравенств.
Графическое решение неравенств с одним неизвестным.
Графическое решение систем неравенств с двумя неизвестными.
Пересечение решений.
Графическое представление функций позволяет приближённо решать неравенства с одним неизвестным и системы неравенств с одним и двумя неизвестными. Чтобы решить графически неравенство с одним неизвестным,необходимо перенести все его члены в одну часть, т.e. привести к виду:
f ( x ) > 0 ,
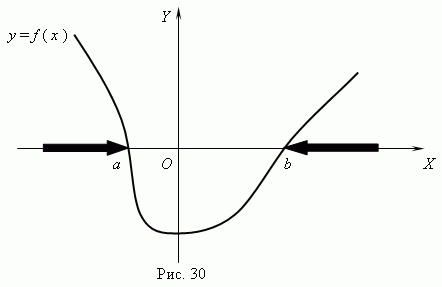
и построить график функции y = f ( x ). После этого, используя построенный график, можно найти нули функции (см. выше), которые разделят ось Х на несколько интервалов. Теперь на основе этого определим интервалы x,внутри которых знак функции соответствует знаку неравенства. Например, нули нашей функции: a и b ( рис.30 ). Тогда из графика очевидно, что интервалы, внутри которых f ( x ) > 0: x < a и x > b ( они выделены жирнымистрелками ). Ясно, что знак > здесь условный; вместо него может быть любой другой: < , ![]() ,
, ![]() .
.
Чтобы решить графически систему неравенств с одним неизвестным, нужно перенести в каждом из них все члены в одну часть, т.e. привести неравенства к виду:
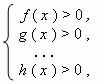
и построить графики функций y = f ( x ), y = g ( x ) , ... , y = h ( x ). Каждое из этих неравенств решается графическим методом, описанным выше. После этого нужно найти пересечение решений всех неравенств, т.e. их общуючасть.
П р и м е р . Решить графически систему неравенств:
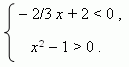
Р е ш е н и е . Сначала построим графики функций y = - 2 / 3 x + 2 и
y = x2 -1 ( рис.31 ):
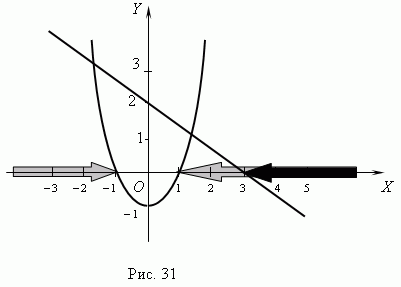
Решением первого неравенства является интервал x > 3, обозначенный на рис.31 чёрной стрелкой; решение второго неравенства состоит из двух интервалов: x < -1 и x > 1, обозначенных на рис.31 серыми стрелками.
Из графика видно, что пересечением этих двух решений является интервал x > 3. Это и есть решение заданной системы неравенств.
Чтобы решить графически систему двух неравенств сдвумя неизвестными, надо:
1) в каждом из них перенести все члены в одну часть, т.e. привести
неравенства к виду:
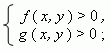
2) построить графики функций, заданных неявно: f ( x, y ) = 0 и g ( x, y ) = 0;
3) каждый их этих графиков делит координатную плоскость на две части:
в одной из них неравенство справедливо, в другой – нет; чтобы решить
графически каждое из этих неравенств, достаточно проверить
справедливость неравенства в одной произвольной точке внутри любой
части плоскости; если неравенство имеет место в этой точке, значит
эта часть координатной плоскости является его решением, если нет – то
решением является противоположная часть плоскости;
4) решением заданной системы неравенств является пересечение
(общая область) частей координатной плоскости.
П р и м е р . Решить систему неравенств:
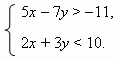
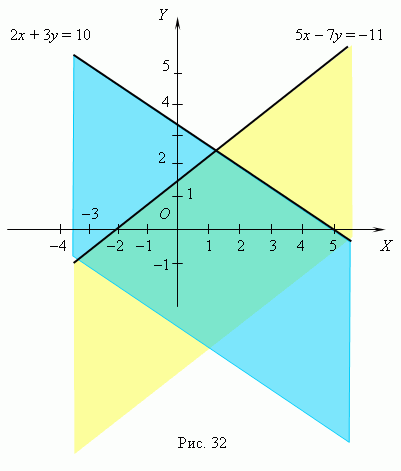
Р е ш е н и е . Сначала строим графики линейных функций: 5x – 7y = -11 и
2x + 3y = 10 ( рис.32 ). Для каждой из них находим полуплоскость,
внутри которой соответствующее заданное неравенство
справедливо. Мы знаем, что достаточно проверить справедливость
неравенства в одной произвольной точке области; в данном
случае легче всего использовать для этого начало координат O ( 0, 0 ).
Подставляя его координаты в наши неравенства вместо x и y,
получим: 5 · 0 – 7 · 0 = 0 > -11, следовательно, нижняя
полуплоскость ( жёлтого цвета ) является решением первого
неравенства; 2 · 0 + 3 · 0 = 0 < 10, поэтому второе неравенство
имеет своим решением также нижнюю полуплоскость ( голубого
цвета ). Пересечение этих полуплоскостей ( область цвета бирюзы )
является решением нашей системы неравенств.