Приближённое решение уравнений.

Графическое решение уравнений с одним неизвестным.

Графическое решение систем уравнений с двумя неизвестными.

 

 

Графическое представление функций позволяет приближённо решить любое уравнение с одним неизвестным и систему двух уравнений с двумя неизвестными. Чтобы решить систему двух уравнений с двумя неизвестными   x   и  y, мы рассматриваем каждое из уравнений как функциональную зависимость между переменными  x  и  y   и строим графики этих двух функций. Координаты точек пересечения этих графиков дают нам искомые значения неизвестных  x  и  y  ( т.e. решение этой системы уравнений ).

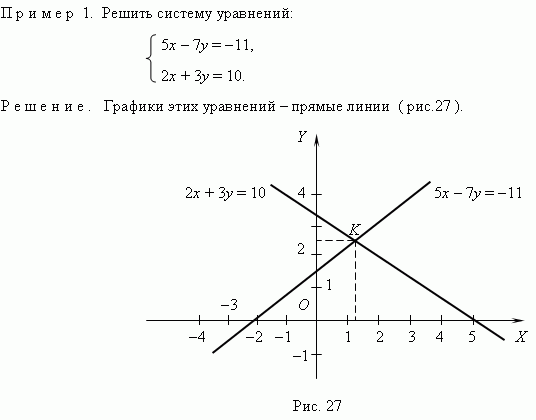
                          В соответствии с графиками координаты точки пересечения

                          K  приближённо равны:  x = 1.25,   y = 2.5.  Точное решение

                          этой системы уравнений:

 

                              

 

 

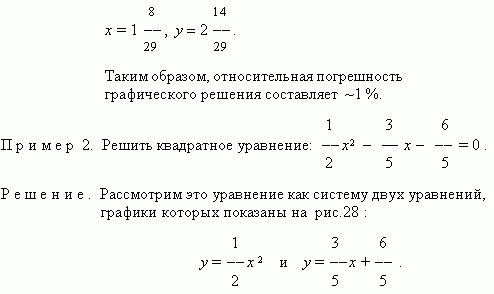
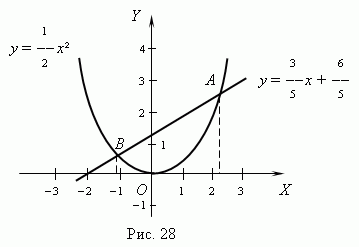
                         После построения графиков находим абсциссы точек

                         пересечения  A и  B:  x₁ » 2.25,  x₂ » -1.1. Точные значения

                         корней этого уравнения:

 

 

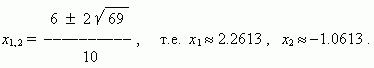
                         Относительная погрешность графического решения в этом

                         примере  ~3.5 %.

 

Чтобы решить графически уравнение с одним неизвестным, необходимо перенести все его члены в одну часть, т.e. привести к виду:

 

f ( x ) = 0 ,

 

и построить график функции  y = f ( x ). Абсциссы точек пересечения графика с осью Х  будут корнями этого уравнения ( нулями этой функции ).

 

                                 

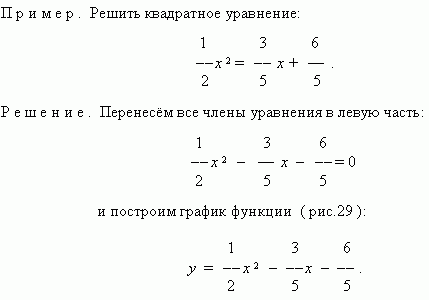
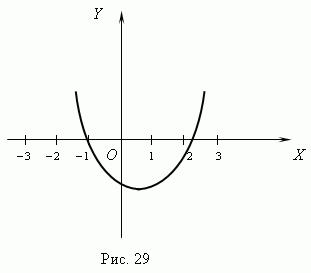
                     По этому графику находим нули функции:  x₁ » 2.25,  x₂ » -1.1.