Параллелограмм. Свойства и признаки параллелограмма.

Прямоугольник. Основные свойства прямоугольника. Ромб.

Квадрат. Трапеция. Средние линии трапеции и треугольника.

 

 

Параллелограмм ( ABCD, рис.32 ) – это четырёхугольник, противоположные стороны которого попарно параллельны.

 

 

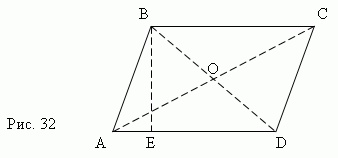
Любые две противоположные стороны параллелограмма называются его основаниями, а расстояние между ними – высотой  ( BE,  рис.32 ).

 

Свойства параллелограмма.

 

1.  Противоположные стороны параллелограмма равны ( AB = CD, AD = BC ).

 

2.  Противоположные углы параллелограмма равны (  A =  C,  B =  D ).

 

3.  Диагонали параллелограмма делятся в точке их пересечения пополам  ( AO = OC, BO = OD ).

 

4.  Сумма квадратов диагоналей параллелограмма равна сумме квадратов его четырёх сторон:

                               
AC² + BD² = AB² + BC² + CD² + AD² .

 

Признаки параллелограмма.

 

Четырёхугольник является параллелограммом, если выполняется одно из следующих условий:

 

 1.  Противоположные стороны попарно равны ( AB = CD, AD = BC ).

   

 2.  Противоположные углы попарно равны (  A =  C,  B =  D ).

   

 3.  Две противоположные стороны равны и параллельны ( AB = CD, AB || CD ).

 

 4.  Диагонали делятся в точке их пересечения пополам  ( AO = OC, BO = OD ).

 

Прямоугольник.

 

Если один из углов параллелограмма прямой, то все остальные углы также прямые ( почему ?). Такой параллелограмм называется прямоугольником  ( рис.33 ) .

 

 

 

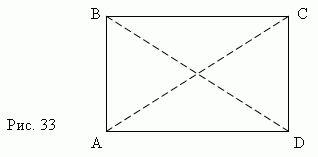
Основные свойства прямоугольника.

 

Стороны прямоугольника являются одновременно его высотами.

 

Диагонали прямоугольника равны: AC = BD.

 

Квадрат диагонали прямоугольника равен сумме квадратов его сторон ( см. выше теорему Пифагора ):

 

AC ²  = AD ² + DC ²  .

 

Ромб. Если все стороны параллелограмма равны, то этот параллелограмм называется ромбом ( рис.34 ) .

 

 

 

 

 

 

 

 

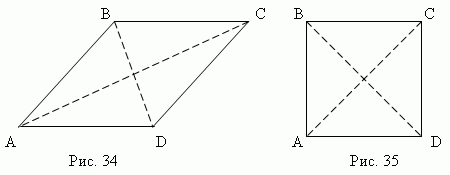
Диагонали ромба взаимно перпендикулярны ( AC  BD ) и делят их углы пополам ( DCA =  BCA,  ABD =  CBD и т.д. ).

 

Квадрат – это параллелограмм с прямыми углами и равными сторонами ( рис.35 ). Квадрат является частным случаем прямоугольника и ромба одновременно;  поэтому он обладает всеми их вышеперечисленными свойствами.

 

Трапеция - это четырёхугольник, у которого две противоположные стороны параллельны ( рис.36 ).

 

 

 

 

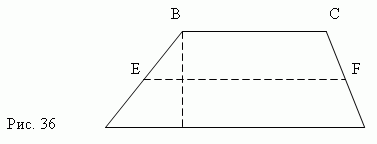
Здесь AD || BC.  Параллельные стороны называются основаниями трапеции, а две другие ( AB и CD ) – боковыми сторонами. Расстояние между основаниями ( BM ) есть высота. Отрезок EF, соединяющий средние точки E  и  F

боковых сторон, называется средней линией трапеции. Средняя линия трапеции равна полусумме оснований:

 

 

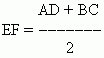
и параллельна им:  EF || AD  и  EF || BC.

 

Трапеция с равными боковыми сторонами ( AB = CD ) называется равнобочной трапецией. В равнобочной трапеции углы при каждом основании равны (  A =  D,  B =  C ).

Параллелограмм может рассматриваться как частный случай трапеции.

 

Средняя линия треугольника – это отрезок, соединяющий средние точки боковых сторон треугольника. Средняя линия треугольника равна половине его основания и параллельна ему. Это свойство вытекает из предыдущего

пункта, так как треугольник может рассматриваться как случай вырождения трапеции, когда одно из её оснований превращается в точку.