Меню сайта

Наш опрос
Оцените мой сайт Отлично Хорошо Неплохо Плохо Ужасно Результаты \| Архив опросов Всего ответов: 12

Статистика
Всего пользователей: 2 Новых за месяц: Новых за неделю: Новых вчера: Новых сегодня:

Основные свойства производных и дифференциалов

Основные свойства производных и дифференциалов.

Производная сложной функции.

Если u ( x ) ≡ const , то

u’ ( x ) ≡ 0 , du ≡ 0.

Если u ( x ) и v ( x ) - дифференцируемые функции в точке x₀ , то:

( c u )’ = c u’ , d ( c u ) = c du , ( c – const );

( u ± v )’ = u’ ± v’ , d ( u ± v ) = du ± dv ;

( u v )’ = u’ v + u v’ , d ( u v ) = v du + u dv ;

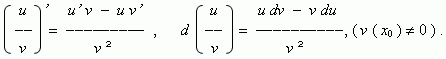
Производная сложной функции. Рассмотрим сложную функцию, аргумент которой также является функцией:

h ( x ) = g ( f ( x ) ).

Если функция f имеет производную в точке x₀, а функция g имеет производную в точке f ( x₀ ), то сложная функция h также имеет производную в точке x₀ , вычисляемую по формуле:

h’ ( x₀ ) = g’ ( f ( x₀ ) ) · f’ ( x₀ ) .

Реклама

Вход на сайт

Поиск

Календарь

Друзья сайта
Официальный блог Сообщество uCoz FAQ по системе Инструкции для uCoz

Бесплатный конструктор сайтов — uCoz

EzDz

Основные свойства производных и дифференциалов