Зеркальная симметрия. Плоскость симметрии.
Центральная симметрия. Центр симметрии.
Симметрия вращения. Ось симметрии. Осевая симметрия.
Примеры вышеупомянутых видов симметрии.
Симметрия плоских фигур. Зеркально-осевая симметрия.
Примеры симметрии плоских фигур.
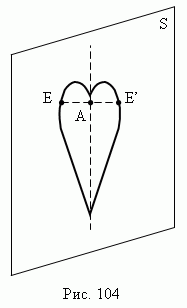
Зеркальная симметрия. Геометрическая фигура называется симметричной относительно плоскости S ( рис.104 ), если для каждой точки E этой фигуры может быть найдена точка E’ этой же фигуры, так что отрезок EE’перпендикулярен плоскости S и делится этой плоскостью пополам ( EA = AE’ ). Плоскость S называется плоскостью симметрии. Симметричные фигуры, предметы и тела не равны друг другу в узком смысле слова ( например, левая перчатка не подходит для правой руки и наоборот ). Они называются зеркально равными.
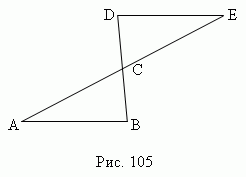
Центральная симметрия. Геометрическая фигура ( или тело ) называется симметричной относительно центра C ( рис.105 ), если для каждой точки A этой фигуры может быть найдена точка E этой же фигуры, так что отрезок
AE проходит через центр C и делится в этой точке пополам ( AC = CE ). Точка C называется центром симметрии.
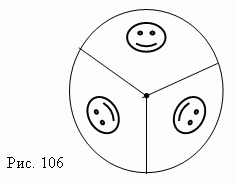
Симметрия вращения. Тело ( фигура ) обладает симметрией вращения ( рис.106 ), если при повороте на угол 360°/n ( здесь n – целое число ) вокруг некоторой прямой AB ( оси симметрии ) оно полностью совпадает со своим
начальным положением. При n = 2 мы имеем осевую симметрию. Треугольники ( рис.105 ) имеют также осевую симметрию.
Примеры вышеупомянутых видов симметрии.
Шар ( сфера ) обладает и центральной, и зеркальной, и симметрией вращения. Центром симметрии является центр шара; плоскостью симметрии является плоскость любого большого круга; осью симметрии – диаметр шара.
Круглый конус обладает осевой симметрией; ось симметрии – ось конуса.
Прямая призма обладает зеркальной симметрией. Плоскость симметрии параллельна её основаниям и расположена на одинаковом расстоянии между ними.
Симметрия плоских фигур. Зеркально-осевая симметрия. Если плоская фигура ABCDE ( рис.107 ) симметрична относительно плоскости S ( что возможно, если только плоская фигура перпендикулярна плоскости S ), то прямаяKL, по которой эти плоскости пересекаются, является осью симметрии второго порядка фигуры ABCDE. В этом случае фигура ABCDE называется зеркально-симметричной.
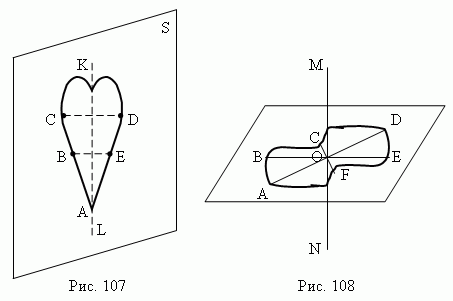
Центральная симметрия. Если плоская фигура ( ABCDEF, рис.108 ) имеет ось симметрии второго порядка, перпендикулярную плоскости фигуры ( прямая MN, рис.108 ), то точка O, в которой пересекаются прямая MN и плоскость фигуры ABCDEF, является центром симметрии.
Примеры симметрии плоских фигур.
Параллелограмм имеет только центральную симметрию. Его центр симметрии – точка пересечения диагоналей.
Равнобочная трапеция имеет только осевую симметрию. Её ось симметрии – перпендикуляр, проведенный через середины оснований трапеции.
Ромб имеет и центральную, и осевую симметрию. Его ось симметрии – любая из его диагоналей; центр симметрии – точка их пересечения.
Круг имеет … Что вы можете сказать о видах симметрии круга ?