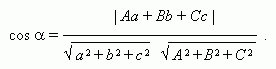Уравнение прямой, проходящей через две различные точки.
Параметрическое уравнение прямой. Уравнение линии
пересечения плоскостей. Условие параллельности прямых.
Условие перпендикулярности прямых. Угол между прямыми.
Угол между прямой и плоскостью.
Уравнение прямой, проходящей через две различные точки ( х1, у 1, z 1 ) и ( х2, у 2 , z 2 ):
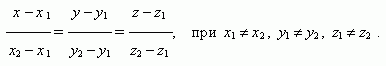
Параметрическое уравнение прямой, проходящей через точку ( х0 , у 0 , z 0 ) и параллельной направляющему вектору прямой ( a, b, с ) :
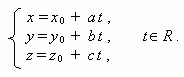
Пусть заданы две плоскости Ах+ Ву+ Сz+ D = 0 и Eх+ Fу+ Gz+ H = 0, причём их нормальные векторы неколлинеарны, тогда система уравнений
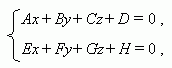
описывает прямую – линию пересечения этих плоскостей.
Пусть ( a, b, с ) и ( p, q, r ) – направляющие векторы двух прямых, тогда имеем условие параллельности прямых:
aq – bp = br – cq = ar – cp = 0 ,
условие перпендикулярности прямых:
ap + bq + cr = 0 ,
угол ![]() между прямыми:
между прямыми:
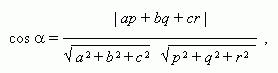
угол ![]() между прямой и плоскостью:
между прямой и плоскостью: